1、麦克斯韦方程组简介
1.1、麦克斯韦方程组积分形式
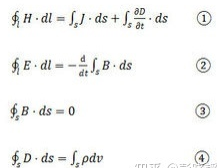
式①含义是：磁场强度H沿任意闭合曲线的线积分，等于穿过此曲线限定面积的全电流。等号右边第一项是传导电流．第二项是位移电流。
式②含义是：电场强度E沿任意闭合曲线的线积分等于穿过由该曲线所限定面积的磁通对时间的变化率的负值。
式③含义是：对于任意一个闭合曲面，有多少磁通进入曲面就有同样数量的磁通离开。
式④含义是：在时变的条件下，从任意一个闭合曲面出来的电通量D的净通量，应等于该闭曲面所包围的体积内全部自由电荷之总和。
1.2、麦克斯韦方程组微分形式
式⑤含义是：磁场强度H的旋度等于该点的全电流密度，即磁场的漩涡源是全电流密度，位移电流与传导电流一样都能产生磁场。
式⑥含义是：电场强度E的旋度等于该点磁通密度B的时间变化率的负值。
式⑦含义是：磁通密度B的散度恒等于零，即B线是无始无终的。
式⑧含义是：在时变条件下，电位移D的散度仍等于该点的自由电荷体密度。
2、麦克斯韦方程组的基础
麦克斯韦方程组的基础有二：一是库仑定律；二是毕奥——沙伐尔定律。
2.1、库仑定律
其中：F为库仑力；K为库仑常数；q1、q2分别为两个点电荷的电荷量；r为两个点电荷间的距离。
当令q2=1时，（公式1）就可修改为电荷q1产生的电场强度公式：
2.2、毕奥——沙伐尔定律
其中: I 是源电流; L 是积分路径; dI 是源电流的微小线元;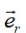
为电流元指向待求场点的单位
向量; μo为真空磁导率，其值为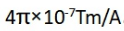
二、麦克斯韦方程组的适用范围
1、麦克斯韦方程组的基础库仑定律的适用范围
库仑定律仅适用于电荷静止且电荷量固定不变的点电荷，当电荷运动或电荷量变化时，由于电场的传递速度是有限的，其与其他不同距离上的电荷发生相互作用所需要的时间就会不同。因此，当电荷运动或电荷量变化时，就必须对库仑定律进行升级修正。
1.1、假设点电荷Q沿X轴以速度V运动，t=0时正好位于坐标原点，如下图所示：
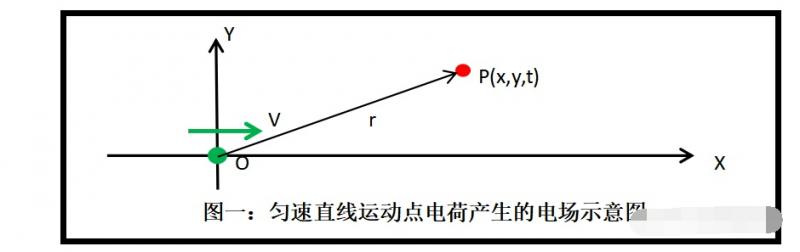
设电场的传递速度为C，则有：
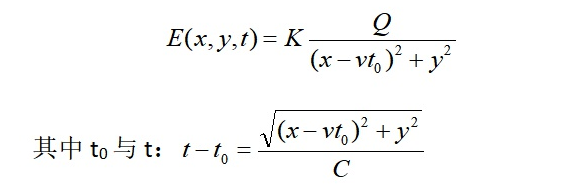
（公式3）
由（公式3）可知：当点电荷运动时，在空间不同位置上的电场是随时间变化的，这种变化还不是同步的，会随距离的增大而滞后。这可能就是所谓的光的传递速度的实质了。
1.2、假设点电荷Q沿X轴方向以位移量S=ASin2πft在区间[-A，A]运动，t=0时正好位于坐标原点，如下图所示：
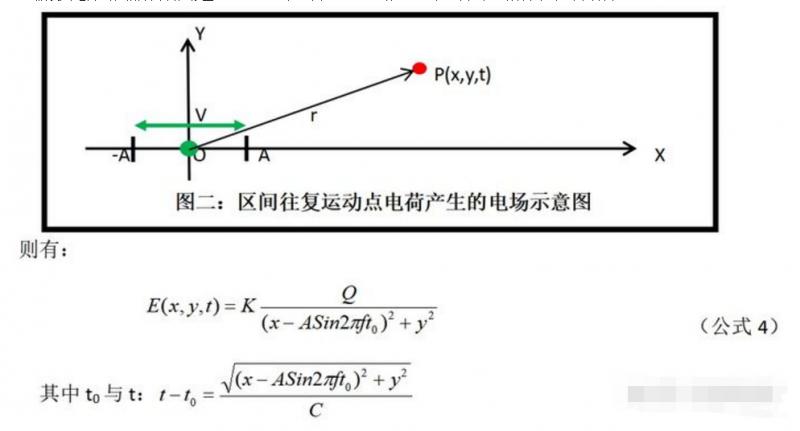
2、麦克斯韦方程组的基础毕奥——沙伐尔定律的适用范围
如库仑定律一样，仅适用于恒定电流且位置固定不变的电流线元，当电流线元运动或电流量变化时，由于磁场的传递速度是有限的，其在不同距离上产生的磁场就会不同，且随距离的变化存在滞后性。因此，当电流线元运动或电流量变化时，就必须对比奥——沙伐尔定律进行升级修正。在此暂不详述。
3、麦克斯韦方程组的适用范围
3.1、积分形式
由于库仑定律和毕奥——沙伐尔定律仅适用于静止且恒定不变的场源（电荷/电流线元），因此，当场源运动且强度随时间变化时，将导致麦克斯韦方程组中的闭合线积分或面积分的结果与静电场和恒定磁场时不同。所谓的线路或面积积分中不同闭合线路或面上的电场和磁场强度均是随时间变化的，即同一闭合线路上在同一时刻的电磁场并不是由场源同一时刻产生的，其磁通量、电流量等随时间的变化也不是单一时刻产生的。这就导致了方程组中的各等式不再成立。
如：将（公式4）代入积分形式的麦克斯韦方程组②号公式左侧，则有：
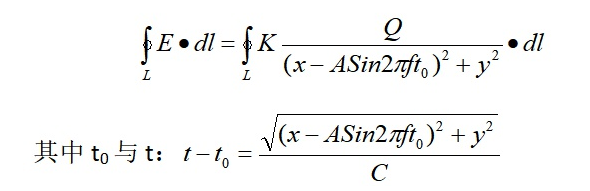
（公式5）
由（公式5）可知，由于决定空间位置的x,y数值不同，t和t0时刻就不同。即同一闭合线路L上不同位置点上的同一时刻的电场是由不同时刻点电荷产生的。同样地，不同闭合线路L上各点同一时刻的电场也是由不同时刻点电荷产生的。因此，闭合线路积分会因闭合线路的不同而不同，其积分结果并不是定值。这是恒定电场时不会有的情形。
由以上叙述可知：积分形式的麦克斯韦方程组与库仑定律和毕奥——沙伐尔定律一样，仅适用于静止场源产生的恒定电场和磁场的情形。当场源运动且场强随时间变化时，方程组不再适用。
3.2、微分形式
由于微分形式削除了场源与计算点间的空间距离，对于点场源而言是成立的。但理想的点场源并不存在，计算点与场源不同部分间仍然存在一定的距离，在场的传递速度有限的情况下，仍然会存在一定的差异，特别是在场源的变化幅度与频率较大时，微分形式仍然难以严格成立。
三、麦克斯韦方程组的适用范围的物理意义
1、利用麦克斯韦方程组推导出来的电磁波有待验证
1.1、将麦克斯韦方程组扩大到时变电磁场是超范围应用
麦克斯韦方程组仅适用于静电场和恒定磁场，而所谓的电磁波是随时间变化的电场和磁场。因此，利用麦克斯韦方程组推导出来的所谓电磁波是值得进一步研究的。
1.2、真空中变化的电场与磁场并不能相互激励和转换而形成所谓的电磁波
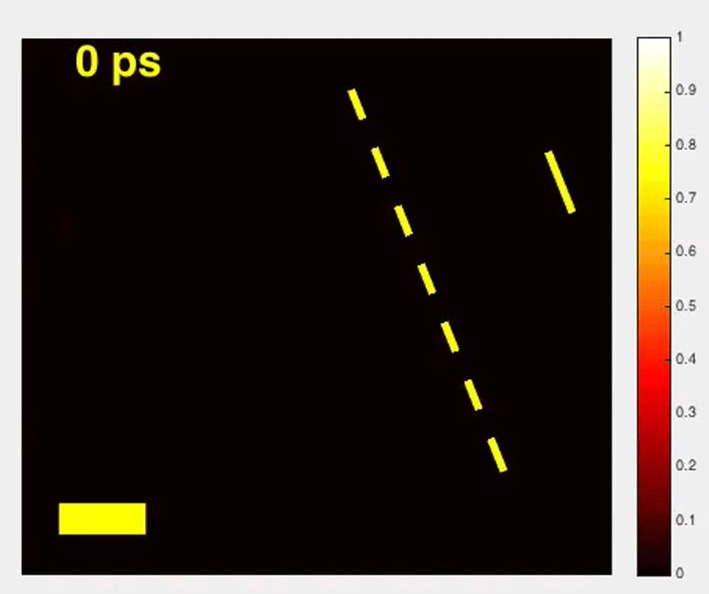
图三：球状光脉冲在介质和真空中传递的动图
上面的动图中虚线与实线间为真空，球状光脉冲在此区域不可侧视证明：光在真空中并不能产生散射或相互激励的次生光。
1.3、地球表面存在黑夜是变化电磁场不能相互激励产生电磁波的重要证据
当地球进入黑夜后，地面上空一定高度范围内仍然存在太阳光产生的变化电场和磁场，但它们并没有像麦克斯韦方程组所预想的那样产生电磁波并照亮地面。这充分证明了在真空中的变化电场并不能感生磁场，同样地，变化的磁场也不能感生电场。这就从根本上否定了电磁波的存在。
2、物理公式和定律都存在适用范围，超出范围就会出现真理变成谬论的可能性
麦克斯韦方程组中的电场、磁场、电流量、磁通量等都是由静止或匀速运动的电荷产生的、不随时间变化的物理量。当电荷运动且数量发生变化时，则这些物理量都会与时间直接相关了，且比静止或匀速运动的电荷时的情况复杂得多。特别需要指出的是：电场和磁场并不能脱离电荷而单独存在。而场论却把场当成了独立于场源而存在的实体来加以研究，这是完全不正确的。
3、由麦克斯韦方程组推导出来的光速仅适用于相对光源/电荷静止时的情形
由于麦克斯韦方程组是由静止电荷和恒定电流条件下导出的光速，因此，其适用范围最多也仅适用于相对光源/电荷静止时的情形。也就是说，由麦克斯韦方程组推导出来的光速并不适用于运动光源的情形。
下式为麦克斯韦方程组推导出的真空中的光速：
其中的ω0和μ0分别为真空中的介电常数和磁导率。
一.麦克斯韦方程组积分形式及其意义
由此可见，麦克斯韦方程组推导出来的光速并不能证明光源运动不会导致光速的变化。也就是说：麦克斯韦方程组并不排斥真空中不同运动状态的光源所产生的光的速度与光源的运动有关。
